Beelden zijn een krachtige manier om concepten over te brengen. In de media lijkt er haast wel een Babylonische spraakverwarring te zijn in de discussie over rekenen. Bij elk gloedvol betoog over rekenen denk ik altijd: ‘Wat zou het achterliggende mentale beeld zijn?’
Ik zal enkele van de meest voorkomende opvattingen beschrijven en voorzien van een typerend beeld. De opvattingen waren in verschillende tijdperken dominant. De genoemde tijdperken zijn uiteraard niet zo scherp afgebakend.
Opvatting 1: 1950-1975 Cijferen
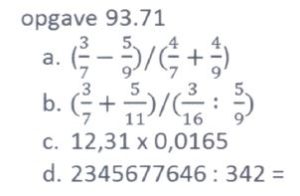 Een vrij persistente opvatting is dat de essentie van rekenen het cijferen is, dat wel zeggen het kunnen uitvoeren van bewerkingen op kale getallen volgens vaste procedures met de hand en op papier: optellen, aftrekken, vermenigvuldigen en delen. De staartdeling is het icoon van deze opvatting. Is dat een relevante bezigheid? In een land dat dreef op handel, scheepvaart en industrie was deze ambachtelijke vaardigheid van het grootste belang. Zonder cijferen geen fabrieken, geen handel, geen zeereizen. Het rekenboek De Cijfferringhe van Willem Bartjens haalde tussen 1600 en 1700 met gemak de honderdste druk. De kwantitatieve kant van de wereld ziet er vandaag heel anders uit en het kale cijferen heeft daarin veel van zijn relevantie verloren.
Een vrij persistente opvatting is dat de essentie van rekenen het cijferen is, dat wel zeggen het kunnen uitvoeren van bewerkingen op kale getallen volgens vaste procedures met de hand en op papier: optellen, aftrekken, vermenigvuldigen en delen. De staartdeling is het icoon van deze opvatting. Is dat een relevante bezigheid? In een land dat dreef op handel, scheepvaart en industrie was deze ambachtelijke vaardigheid van het grootste belang. Zonder cijferen geen fabrieken, geen handel, geen zeereizen. Het rekenboek De Cijfferringhe van Willem Bartjens haalde tussen 1600 en 1700 met gemak de honderdste druk. De kwantitatieve kant van de wereld ziet er vandaag heel anders uit en het kale cijferen heeft daarin veel van zijn relevantie verloren.
Opvatting 2: 1975-2000 Rekenen in context
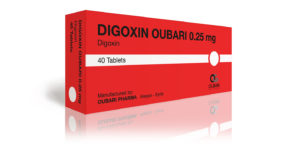 Een andere opvatting luidt dat het bij rekenen vooral gaat om het kunnen oplossen van praktische kwantitatieve problemen. Zo’n probleem moet dan wel gepresenteerd worden in taal of in beeld. Dat noemen we een context. Deze benadering is op dit moment gemeengoed in het onderwijs in Nederland. De huidige schoolboeken en toetsen staan er vol mee. In realistisch reken- en wiskundeonderwijs komen veel van dit soort contextopgaven voor. Maar ook in leergangen die gericht zijn op probleemoplossen, toepassen en modelleren.
Een andere opvatting luidt dat het bij rekenen vooral gaat om het kunnen oplossen van praktische kwantitatieve problemen. Zo’n probleem moet dan wel gepresenteerd worden in taal of in beeld. Dat noemen we een context. Deze benadering is op dit moment gemeengoed in het onderwijs in Nederland. De huidige schoolboeken en toetsen staan er vol mee. In realistisch reken- en wiskundeonderwijs komen veel van dit soort contextopgaven voor. Maar ook in leergangen die gericht zijn op probleemoplossen, toepassen en modelleren.
Opvatting 3: 2000-2025 Gecijferdheid

Wereldwijd wint een derde opvatting snel aan populariteit. Die zegt dat leerlingen gecijferd moeten worden om met de kwantitatieve kant van de wereld om te gaan. Gecijferdheid neemt, meer nog dan realistisch rekenen, de wereld om ons heen als uitgangspunt. Die is zo rijk, zo gevarieerd en soms zo complex, dat leerlingen een zeer uitgebreid repertoire nodig hebben om zich daarin te redden. Bij vermenigvuldigen gaat het niet om een som en een goed antwoord, maar om het herkennen van vermenigvuldigstructuren in bloemperken, stapelingen etc. Bij delen gaat het niet om de staartdeling maar om verdeel- en uitdeelproblemen bij recepten, bij verhoudingen, bij medicatie etc. Maar het gaat bovendien om het trekken van conclusies uit getalsmatige informatie. Interpreteren, analyseren, ordenen, (in)schatten, structureren en selecteren van kwantitatieve informatie zijn vaardigheden die horen bij gecijferdheid. Kortom leerlingen toerusten voor de veelheid aan kwantitatieve verschijningsvormen in de echte wereld.
Mijn uitdaging aan u. Sta de komende maanden bij elk artikeltje dat u leest over rekenen, eens stil wat daarbij de achterliggende, veelal impliciete, opvatting is over rekenen. Mogelijk voelt u zich zelf het meest thuis bij één van deze opvattingen. Ook dat geeft nuance aan de discussie.
Eerder verschenen in 2015 in Euclides 91(2). p.15
