Eerder verschenen in Volgens Bartjens 39-5, hét vaktijdschrift voor rekenen op de basisschool.
Wiskundig leren denken op de basisschool
In eerdere columns voor Volgens Bartjens (38-4 , 38-5, 39-1, 39-2, 39-3 , blog1, blog2) heb ik onderzoeksartikelen over rekenen op de basisschool besproken die zeer recent waren, bijvoorbeeld uit de laatste twee jaar.
Voor dit onderwerp ga ik even terug in de tijd. Er is inmiddels al een heel lange traditie van onderzoek en denkers over rekenonderwijs die onderzocht en benadrukt hebben dat leren van bewerkingen met getallen nooit doel op zich kan zijn. Dat is immers een veel te armoedige, schrale en trucmatige invulling van rekenen in het basisonderwijs. Het fundamentele achterliggende doel van rekenonderwijs is kinderen te leren omgaan met de kwantitatieve wereld om ons heen in al haar verscheidenheid. Maar dan moet die kwantitatieve wereld om ons heen ook systematisch onderdeel uitmaken van de rekenervaringen die kinderen opdoen.
Verbinding maken met de werkelijkheid is één van de belangrijkste factoren in het betekenisvol maken van de leerstof en daarmee van motivatie. Loskoppelen van de werkelijkheid is één van de belangrijkste factoren van vervreemding, psychologische rigiditeit en rekenangst.
John Dewey
McLellan, J. A., & Dewey, J. (1895). The psychology of number and its applications to methods of teaching arithmetic. New York, NY: D. Appleton & Company.
McLellan, J.A. & Ames, A.F. (1899). The Primary Public School Arithmetic. New York, NY: The MacMillan Company
Een van de grote denkers over onderwijs en democratie is John Dewey. John Dewey wordt wel de filosoof van de democratie genoemd. In zijn werk staat de kans op de optimale ontwikkeling voor elk individu centraal, die echter samen gaat met de eis van een grote sociale verantwoordelijkheid van elk individu. Veel onderwijsvernieuwing in de vorige eeuw is gebaseerd op de publicaties van John Dewey. Ook recent en dichtbij, zoals bijvoorbeeld het onderwijsconcept van De Nieuwste School in Tilburg.
Minder bekend is dat Dewey vrij vroeg in zijn carrière een psychologisch standaardwerk over rekenonderwijs schreef , waarbij ook een rekenmethode werd uitgebracht. Hij schreef dit samen met James McLellan, een schoolhoofd en onderwijspsycholoog uit Ontario. In het voorwoord van The Psychology of Numbers schuwt Dewey de duidelijkheid in zijn opvattingen over de mechanische leraar (empiricist) niet:
“The worst thing about empiricism in every department of human activity is that it leads to a blind observance of rule and routine. The mark of the empiric is that he is helpless in the face of new circumstances; the mark of the scientific worker is that he has power in grappling with the new and the untried; he is master of principles which he can effectively apply under novel conditions. The one is a slave of the past, the other is a director of the future. This attachment to routine, this subservience to empiric formula, always reacts into the character of the empiric; he becomes hour by hour more and more a mere routinist and less and less an artist. Even that which he has once learned and applied with some interest and intelligence tends to become more and more mechanical, and its application more and more an unintelligent and unemotional procedure. It is never brightened and quickened by adaptation to new ends. The machine teacher, like the empiric in every profession, thus becomes a stupefying and corrupting influence in his surroundings ; he him-self becomes a mere tradesman, and makes his school a mere machine shop.” (p.9)
En dan laat ik wat hij schrijft over de: “authoritative instruction in methods and devices.” (p.10) nog maar even weg.

Dewey bepleit een integratie van hogere-orde denkvaardigheden zoals generalisatie, abstractie, discriminatie (onderscheid maken) en relaties (of verbanden) leggen. Hij ziet die als vanzelfsprekend passend bij de rijkheid van de cognitieve ontwikkeling die kinderen doormaken in de basisschooltijd. En hij laat in zijn rekenmethode bladzijde na bladzijde zien hoe je dat praktisch kan doen in de klas. In de afbeelding zomaar een bladzijde uit het bijbehorende rekenboek. Echt waar uit 18991).
Tatiana Ehrenfest
Ehrenfest-Afanasjeva, T. (1931). Uebungensammlung zu einer geometrischen propädeuse [Exercises in experimental geometry]. Martinus Nijhoff.
Een vergelijkbare opvatting over de verbinding van rekenen met de werkelijkheid zien we later ook terug bij Tatjana Ehrenfest-Afanasjeva en haar Oefeningenverzameling (1931). Zij richt zich helemaal op een praktische en voor kinderen inspirerende manier om naar meten en meetkunde te kijken, zie afbeelding 2.

Zij zegt over haar methode:
“(..), it cannot be denied that “practical” teaching has more pupils reacting to the taught material with a certain liveliness: at any rate, they see more clearly what it is about, and they are better at picturing spatial objects. The development of the imaginative capacity is also often mentioned in connection with the practical method of instruction.“(p.5-6)
Zij woonde jaren in Leiden, waar onder andere ook Einstein en Freudenthal op bezoek kwamen. Zo kwamen dit soort ideeën ook bij Freudenthal terecht, enzovoorts.
Curriculum.nu
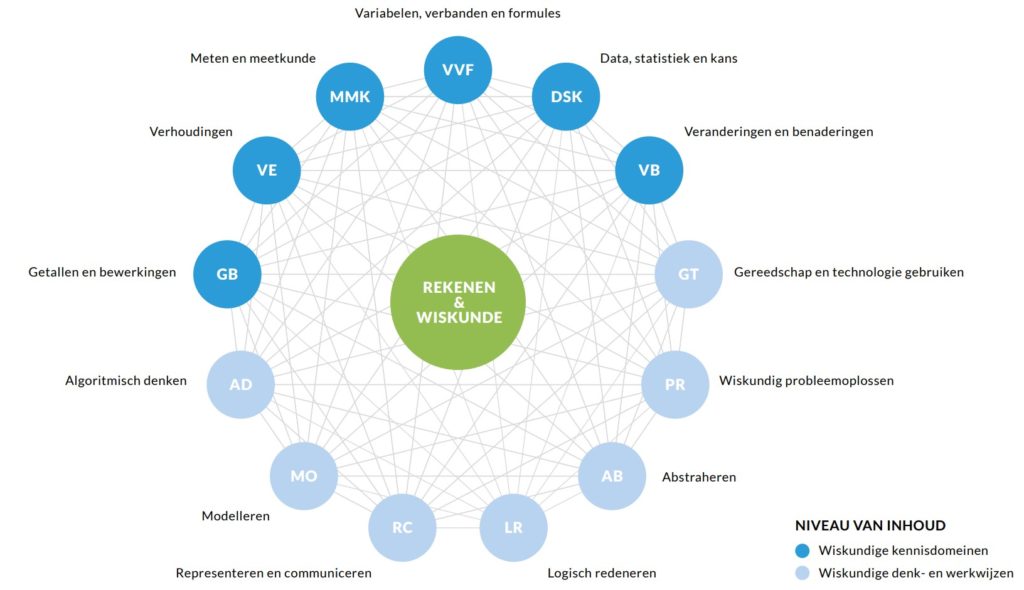
Ik leg nu even de verbinding naar het overkoepelende idee uit de voorlopige opbrengsten van curriculum.nu , zie afbeelding 3: Ontwikkelteam Rekenen Wiskunde (2019). Bouwstenen voor een nieuw curriculum Rekenen en Wiskunde. Website: Curriculum.nu
Ook hier zie je de verscheidenheid van wiskundige domeinen gekoppeld aan hogere-orde vaardigheden, ook voor het basisonderwijs, waar er vooral informeel kennis mee gemaakt kan worden, passend bij de cognitieve ontwikkeling die voor ieder kind plaatsvindt op zijn haar tempo en wijze. Net zoals John Dewey en Tatjana Ehrenfest uitvoerig beschrijven in hun boeken.
Ten slotte
Ik kwam als kritiekpunt op curriculum.nu tegen dat er sprake is van oude wijn in nieuwe zakken. Ik zou het eerder omschrijven als nieuwe wijn uit oude vaten. En zoals we weten is dat het recept voor topwijnen, mits behandeld door experts die dat zorgvuldig en met praktijkervaring verder ontwikkelen. De boeken van John Dewey en Tatjana Ehrenfest kunnen hiervoor als een rijke inspiratiebron dienen.
1) Zie https://www.gecijferdheid.nl/dewey/
Oorspronkelijke column Volgens Bartjens 39-5

