Eerder verschenen in Volgens Bartjens 39-4, hét vaktijdschrift voor rekenen op de basisschool.
Wiskundig denken
Wiskunde voor 3-jarigen? Is dat niet wat overdreven?
Er is maar een land ter wereld dat twee verschillende woorden heeft voor rekenen en wiskunde … [denkpauze]
En dat heeft vérstrekkende gevolgen voor ons collectieve beeld van wat kinderen en jonge kinderen nu precies moeten leren en ontwikkelen op dit gebied. Rekenen is een werkwoord dat in de publieke opinie nog steeds wijdverbreid wordt geassocieerd met uitrekenen, dat wil zeggen met het verkrijgen van een antwoord op een som.
In andere talen heet dat type rekenen “arithmetic”, “calculer” of “rechnen”. In al die landen heet echter het schoolvak steevast mathematics, Mathematik, .. of een variant daarop, ook op de basisschool.
Die naamgeving mathematics levert gelijk al een heel andere associatie op. Wiskunde is de wetenschap van getallen, patronen en structuren. Daarmee is dan ook het verband gelegd met de domeinen uit het referentiekader rekenen.
- Getallen zitten in alle domeinen, maar vooral in het domein getallen 🙂
- Patronen is verbonden met het domein verbanden;
- Structuren vind je veel in het domein meetkunde, in het domein verhoudingen en op het snijvlak van de domeinen getallen en meten.
Zo zie je dat alle domeinen van het referentiekader en van de kerndoelen de ontwikkeling van wiskundig denken van kinderen als uitgangspunt hebben. Een uitgebreide verkenning van getallen en bewerkingen en het gebruik van getallen in het dagelijkse leven hoort daar natuurlijk ook bij.
Het jonge kind
Er zijn sterke aanwijzingen dat ons brein hardwired is voor wiskundig denken. Zie bijvoorbeeld de interessante boeken van Butterworth (1999) of Devlin (1996). Niet zo vreemd: wiskunde is immers geen buiten de mens bestaand kennisdomein dat ontdekt moet worden. Het is een systeem van geabstraheerde en gegeneraliseerde menselijke ervaringen. Daarom is een ervaringsbasis, de werkelijkheid, contexten, zo vanzelfsprekend bij het leren van reken-wiskunde.
Kinderen beginnen de ontwikkeling van hun reken-wiskundig denken al direct na de geboorte, eigenlijk zodra ze kunnen waarnemen. En een basaal gevoel voor aantallen (een ding is iets anders dan twee dingen) zit diep verankerd in onze hersenstam. Zelf dieren hebben dit onderscheidend vermogen. Het was evolutionair blijkbaar handig om een zeker mate van number sense en gevoel voor ruimtelijk oriënteren te hebben.
In de voorschoolse periode maken kinderen al grote ontwikkelingen door op dit gebied, zeker als ze gaan kruipen en lopen. En zeker als ze met blokken gaan spelen.
Dit wiskundig denken kan op school in de eerste groepen gericht verder ontwikkeld worden door kinderen een rijke leeromgeving te bieden met veel uitdagingen om op een speelse manier aan de gang te gaan met aantallen, met hoeveelheden, met tellen, met tekenen, met klimmen (oriënteren in de ruimte) en met patronen.
Jonge kinderen kunnen ontzettend veel plezier beleven aan het ontwikkelen van hun reken-wiskundig denken. Zolang je maar wegblijft van formele notaties, van instructie, van het uitrekenen van sommen en van praten in termen van goed/fout. Goede vragen stellen om de verwondering aan te wakkeren of de aandacht ergens op te richten is de cruciale didactiek.
Het is goed te bedenken dat iets als rekenangst geen leerlingkenmerk is, maar een product van onderwijs. Rekenangst ontstaat op school door rekenen te associëren met selectie, met achterstand, met goed-fout en en door te vroege blootstelling aan te formele, te abstracte en te eenvormige rekenlesjes.
In eerdere nummers van Volgens Bartjens (38-4 , 38-5, 39-1, 39-2, 39-3 , blog1, blog2) heb ik al enkele onderzoeken aangehaald die betrekking hadden op de ontwikkeling van reken-wiskundig denken van het jonge kind.
Eentje over de rol die ICT hierbij zou kunnen spelen als er gekozen wordt voor een heel speelse benadering (38-4). En eentje hoe het werken aan patronen en ruimtelijk figuren een positief effect heeft op het latere schoolsucces bij rekenen en wiskunde (38-4). En eentje die het positieve effect heeft gemeten van het gebruik van Building Blocks door jonge kinderen (38-5)
Twee recente artikelen
Ik bespreek nog kort twee artikelen die zeer recent zijn verschenen.
Are children’s spontaneous number focusing tendencies related to their home numeracy environment?
Sanne Rathé, Joke Torbeyns, Bert De Smedt, Lieven Verschaffel ZDM, January 2020
Een belangrijke factor voor rekensucces is de mate waarin kinderen spontaan hun aandacht richten op aantallen, getallen en patronen en verbanden (spontaneous focus on …).. In dit onderzoek is onderzocht of de thuissituatie (rijk aan gecijferdheidssituaties of niet) een verklarende factor zou kunnen zijn voor de grote verschillen in spontane aandacht die er tussen kinderen worden aangetroffen.
Dat is natuurlijk een plausibele hypothese. Veel aspecten van schoolsucces hangen immers samen met de afkomst van kinderen. In dit onderzoek blijkt de thuissituatie op dit specifieke fenomeen niet een significante factor te zijn. Wat dan wel, is een belangrijk vraag voor vervolgonderzoek, want de spontane aandacht heeft wel effect op het latere rekensucces.
Preschoolers’ diferent ways of structuring part‑part‑whole relations with fnger patterns when solving an arithmetic task
Angelika Kullberg, Camilla Björklund; ZDM, December 2019
Kinderen blijken op verschillende manieren hun vingers te gebruiken als ondersteuning voor optelsommen. Dit is een onderzoekje dat je zo ook in de klas kan doen.
In het experiment werden kinderen (5- en 6- jarigen) aangemoedigd hun vingers te gebruiken. Vervolgens werd mondeling de volgende vraag gesteld:
“Je hebt drie glazen, maar je moet de tafel dekken voor 8 personen. Hoeveel glazen erbij heb je dan nog nodig?”
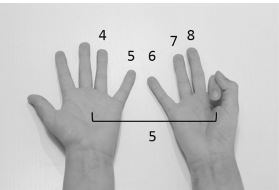
Hieronder twee fotootjes uit het artikel.
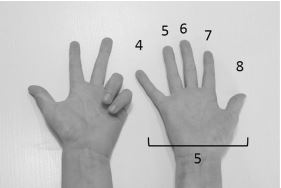
In de linkerfiguur laten kinderen 3 zien en tellen door op hun andere hand en concluderen op zicht en direct dat 5 het antwoord is.
In de rechterfiguur laten kinderen 3 zien en tellen vervolgens door tot 8 te komen, Vaak moeten ze dan weer 1 tot 5 tellen om tot een conclusie te komen. Probeer het maar eens uit in de klas.
Zo’n onderscheid geeft waardevolle informatie of kinderen al een vijf-structuur zien, herkennen en gebruiken met grotere kans op rekensucces later.
Kortom een pleidooi om altijd goed naar het eigen denken en handelen van kinderen te blijven kijken. Zonder dat kun je met een instructiewals alles zomaar plat walsen.
Aanbevolen literatuur:
Butterworth, B. (1999). The mathematical brain. London, UK: Macmillan. Retrieved from http://www.mathematicalbrain.com/
Devlin, K. (1996). Mathematics: The Science of Patterns: The Search for Order in Life, Mind and the Universe. Scientific American Paperback Library.
Oorspronkelijke column Volgens Bartjens 39-4

