Eerder verschenen in Volgens Bartjens 39-3.
Wetenschappelijke resultaten worden in sommige kringen gezien als de ultieme bron van kennis, omdat er transparant, systematisch, en repliceerbaar data wordt geproduceerd op basis waarvan valide conclusies worden getrokken.
In sociaalwetenschappelijk onderzoek, waartoe onderwijsonderzoek behoort, is daar nogal wat op af te dingen. In elke onderwijssituatie is het aantal variabelen dat een rol speelt zeer groot. Het is vrijwel onmogelijk om enkele variabelen te isoleren en daartussen een causaal verband aan te tonen. Hoe graag de onderzoeker dat ook wil.
En je kunt je ook wel voorstellen dat onderwijsonderzoek eigenlijk nooit repliceerbaar is: “Volgend jaar doen we dit weer in een groep 6, weer in december, weer bij dit onderwerp, weer met deze docent….?” En dan denken dat je identieke situaties hebt?
Kortom, zodra in presentaties of discussies over onderwijsonderzoek iemand “bewezen” zegt of “evidence-based” of “uit onderzoek is gebleken”, dan is het zaak om op te gaan letten. Of juist niet meer.
Heeft onderwijsonderzoek dan wel waarde? Zeker, heel veel! Kennis nemen van wetenschappelijke onderzoeksresultaten kan op ideeën brengen voor nieuwe aanpakken of proeftuintjes, kan inspireren, kan nieuwe aanpakken onderbouwen, en kan een rol spelen bij beslissingen over het rekenbeleid op school. Dat heet dan “evidence-informed” of nog liever mijn favoriet ”evidence-inspired”.
Leraren toegang tot wetenschappelijke publicaties
Het is zeer toe te juichen dat sinds kort leraren gratis toegang hebben tot wetenschappelijke publicaties via de EBSCO-Education Source database. Tot voor kort zat 90% van publicaties over onderwijsonderzoek achter een “betaalmuur” van grote commerciële uitgeversconcerns. Wat natuurlijk merkwaardig is voor onderzoek dat wordt uitgevoerd met gemeenschapsgeld.
Bent u geïnteresseerd om eens rond te snuffelen wat er zoal wordt onderzocht en gepubliceerd, dan kunt u zich aanmelden bij de website voordeleraar.nl Voorlopig is het voor een jaar (tot eind oktober 2020) geregeld, maar ik kan me niet voorstellen dat het niet wordt gecontinueerd.
Zoeken in publicaties
Met toegang ben je er nog niet. Mocht je naar aanleiding van dit en vorig nummer van Volgens Bartjens geïnteresseerd zijn in voorbeelden van onderzoek naar statistiek in de basisschool, dan zou je kunnen zoeken op statistics, primary, and education. Maar dan krijg je alle artikelen waarin het woord statistics voorkomt en dat zijn ze eigenlijk vrijwel allemaal. Dus enige bedrevenheid in het gebruik van goede zoektermen is wel van belang. Ik zou het eens proberen met “statistical literacy” en ”primary eduation” en dan van de afgelopen twee jaar. Ik kwam zo bijvoorbeeld de volgende twee artikelen tegen.
Primary school students’ reasoning when comparing groups using modal clumps, medians, and hatplots. Daniel Frischemeijer. Mathematics Education Research Journal, December 2019, Volume 31, Issue 4, pp 485–505
Leuk onderzoek met leerlingen uit groep 6 en gebruik makend van Thinkerplot (www.tinkerplots.com). Dat is interessante laagdrempelige software om de gegevens van steeds twee groepen te vergelijken, bijvoorbeeld de spronglengte van verschillende soorten papieren kikkers (!). Zie figuur 1
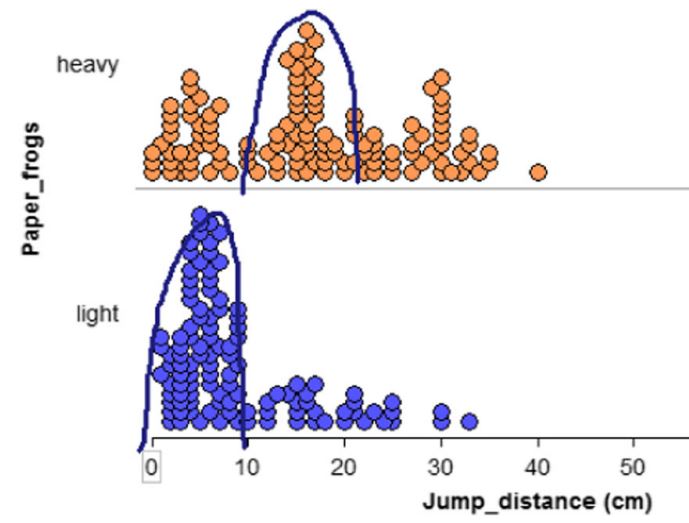
Figuur 1
In het onderzoek wordt vooral gekeken naar hoe kinderen redeneren over het verschil tussen twee groepen en in welke mate ze daarbij informeel gebruik maken van centrum- en spreidingsmaten op basis van grafische representaties die door een computerprogramma worden gegenereerd. Hoe 21e -eeuws wil je het hebben!
De onderzoekers benadrukken nog maar eens de waarde van het eerst informeel verkennen van allerlei wiskundige concepten zonder nog formele taal en notaties te (hoeven) gebruiken:
“Taking into account a broader perspective, for example, the development of statistical reasoning in lower secondary grades (5–10), teachers might build on the proto-concepts of modal clumps and the precursor representation of hatplots prior to students developing more formal concepts like median or boxplots to compare two groups.”
Het is inderdaad van belang te blijven benadrukken dat het bij statistiek op de basisschool vooral gaat om een informele verkenning en een rijke bron om te leren redeneren op basis van getallen (data).
Modelling with authentic data in sixth grade. Lyn D. English & Jane Watson.
ZDM Mathematics Education (2018), Volume 50, pp. 103–115
Interessant in dit onderzoek is dat er gebruik wordt gemaakt van authentieke data. Daarmee komt het heel dichtbij wat je leerlingen zou willen meegeven aan kritisch vermogen in het omgaan met data “voor als ze later groot zijn”.
De onderzoekers formuleren het als volgt:
“By undertaking their own investigations and generating different conclusions, primary school students can learn to make critical decisions with data, where variation and uncertainty are ever present. Yet these school students often do not receive the appropriate or adequate experiences that set them on the road to this statistical literacy. Developing statistical literacy takes a long time and must begin in the earliest years of schooling.”
In dit Australische onderzoek stonden de zwemtijden van Australische zwemmers centraal zo rond de Olympische Spelen van 2016. Voor leerlingen was de brede onderzoeksvraag of de prestaties van de Australische zwemmers vooruitgaan of niet. En als dat zo is, hoe groot dan de kans is dat er goud wordt gewonnen op de Olympische Spelen?
U zou zoiets eens moeten doen in een klassengesprek. Het is vaak verrassend te ervaren hoe goed leerlingen in staat zijn om verhelderende subvragen te formuleren en genuanceerd om te gaan met wat dan kans is. De data werden in dit geval gepresenteerd in een matrix waarvan u een stukje ziet in figuur 2
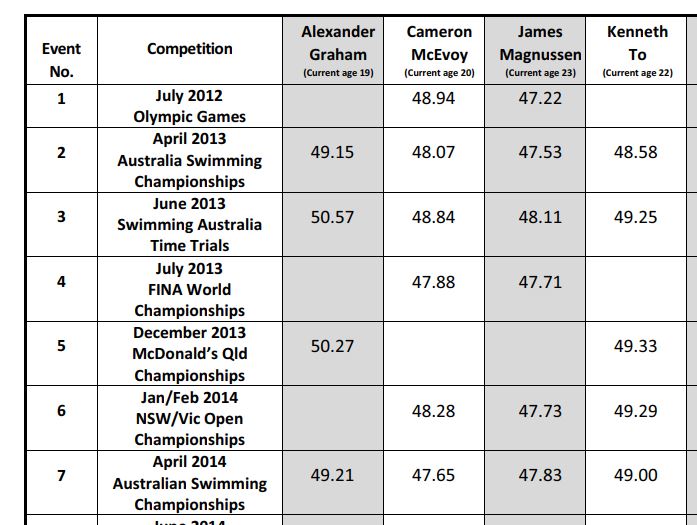
Figuur 2
De groepjes leerlingen verschilden in de hoeveelheid berekeningen die ze gebruikten. Sommige groepjes rekenden veel, andere groepjes gebruikten vrijwel alleen maar redeneringen op basis van de gegeven data. Er ontstond op vrij natuurlijke manier een differentiatie tussen de groepjes en in de groepjes. Zo kunnen de leerlingen zelf een rijke leeromgeving voor elkaar worden.
De onderzoekers merken daar in hun eindconclusies over op:
“Experiences in the primary grades do not usually afford children opportunities to link their mathematical and statistical learning in dealing with problems involving complex data, where the exact nature of a desired end-product is not known in advance, and where different approaches to solution and multiple solutions are possible.”
Dat zouden we inderdaad best vaker kunnen doen.

